Graphing for Straight Lines

You can understand this math by grasping these basics.

JUST KNOW SOME DEFINITIONS AND FORMULAS AND YOU ARE ON YOUR WAY!

Graphs for straight lines are traditionally completed on a coordinate plane. There are two axes: one, horizontal called X axis; the other, vertical called Y axis. The coordinates also called an ordered pair are represented by the notation (x,y).

 

 

BASICS:

  • Axes: X & Y
  • Notation
  • Intercepts
  • Slope
  • Equations

Graph for Straing Lines has four quadrants

 

 

A straight line is either horizontal, vertical, or oblique. For example, look at this diagram.

As you can see there are two directions: with the X values going left and right,  and the y values going from top to bottom on the plane.  A coordinate is the intersection of two points. This is the standard notation to represent a point on the graph: (x,y).  As you know by now the x value reprsents the x axis and the y the y axis.
The notation (x1,y1) and (x2,y2) can respectively represent a set of points such as (2,1) and (3,2). (x,y) without the subscripts is used to represent the variables whose values are to be determined. The values are determined by the equation for the line. (x,0) represents the x-intercept. (0,y) represents the y-intercept. The x-intercept is where the line crosses the x axis and the y-intercept is where the graph's line crosses the y axis.
SLOPE: The slope is a measure for oblique lines on the graph. Thus, oblique straight lines have a slope which is different from 0. Slope is often represented by the constant m. It is the change in the y axis divided by the change in the x axis. EQUATION: Given two points on a line then
m =   y −  y1 ∕ x  −  x1
That is the change in y ÷ x,  
( Δy)   ∕   ( Δx)

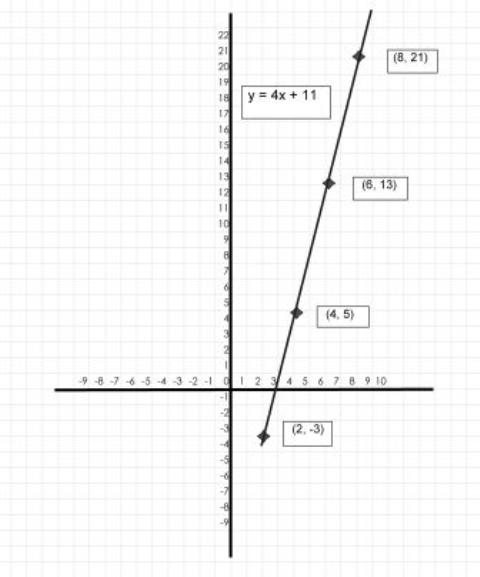
COORDINATES:

X-AXIS Y-AXIS
2 -3
4 5
6 13
8 21

Equation

The general equation of a line through point (2, −3) with a slope 4 is: m =   y −  y1 ∕ x  −  x1 and may be re-written as:
the general equation y −  y1 = m (x  −  x1) and substituting values for the general equations gives you:
y − (−3) = 4(x − 2)
y + 3 = 4x − 8
y = 4x − 11 This equation solves for y.

Graph for Equation y=4x-11

Some Problems

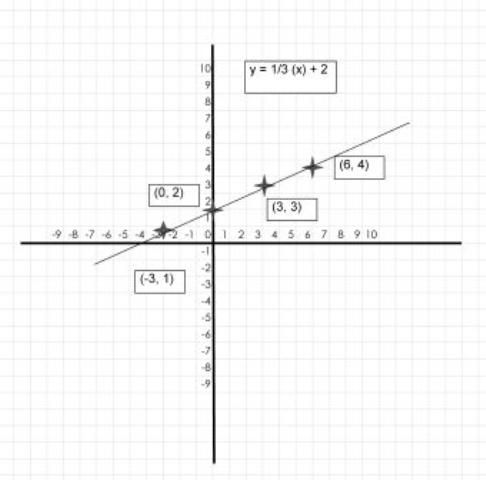
COORDINATES:

X-AXIS Y-AXIS
0 2
-3 1
3 3
6 4

Write and graph the equation of a straight line that passes through the point (0, 2) with a slope of 1⁄3:
m =   y −  y1 ∕ x  −  x1 and may be re-written as:
the general equation y −  y1 = m (x  −  x1) and substituting values for the general equations gives you:
y − 2 = 1⁄3(x − 0)
y = 1⁄3 (x) + 2 This equation solves for y.

Graph for Equation y= 1/3 (x) + 2

Return to Future Index

DELAWARE'S MIDDLETOWN ODESSA AND TOWNSEND AREA